För ett stort utbud av praktiskt användbara fall har forskare vid MIT hittat ett sätt att öka hastigheten på en av de viktigaste algoritmerna inom informationsvetenskaperna: FFT. Den nya algoritmen kan få stor påverkan inom många områden och tillämpningar, till exempel för komprimering av videofiler.

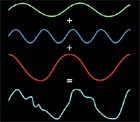
Grafik: Christine Daniloff

Fouriertransform är ett av de mest grundläggande koncepten inom informationsvetenskaperna. Det är en metod för att representera en oregelbunden signal som en kombination av rena frekvenser. Fouriertransform används universellt inom signalbehandling men kan också användas för att komprimera bilder och ljudfiler, lösa differentialekvationer, och sätta priset på aktieoptioner med mera.

Anledningen till att Fouriertransformen är så utbredd är en algoritm som benämns Fast Fourier Transform (FFT) och som utformades i mitten av 1960-talet. FFT gjorde det praktiskt att beräkna Fouriertransformer ”i flykten”. Ända sedan FFT föreslogs har dock folk undrat om ändå inte en ännu snabbare algoritm kunde hittas.

Vid the Association for Computing Machinery:s Symposium on Discrete algoritmer (SODA) denna vecka kommer en forskargrupp vid Massachusetts Institute of Technology (MIT) att presentera en ny algoritm som, inom ett brett utbud av praktiskt viktiga fall, kan förbättra FFT. Under vissa omständigheter uppger MIT att förbättringen kan vara riktigt dramatisk – en tiofaldig ökning av hastigheten. Den nya algoritmen kan vara särskilt användbar för bildkomprimering och till exempel möjliggöra att via smarta telefoner trådlöst kunna överföra stora videofiler utan att för den skull tömma batteriet och för att spara bandbredd.

Precis som för FFT fungerar den nya algoritmen på digitala signaler. En digital signal är bara en serie siffror – diskreta prover (samples) av en analog signal, såsom ljudet från ett musikinstrument. FFT tar en digital signal som innehåller ett visst antal prover och uttrycker det som den ”viktade” summan av ett ekvivalent antal frekvenser.

"Viktade" innebär att vissa av dessa frekvenser räknas mer mot totalen än andra. I själva verket kan många av de frekvenserna ha så låga vikter att de med säkerhet kan lämnas därhän. Det är därför Fouriertransformen är användbar för komprimering. Ett åtta-till-åtta block pixlar kan betraktas som en 64-samplingssignal, och därmed som summan av 64 olika frekvenser. Men såsom forskarna påpekar har empiriska studier visat att man i genomsnitt kan bortse från 57 av dessa frekvenser med en minimal förlust av bildkvalitet.

Signaler som Fouriertransformer inkluderar är ett relativt litet antal tungt viktade frekvenser som kallas "sparce". Den nya algoritmen avgör vikten av en signals tyngst viktade frekvenser, ju ”glesare” (sparcer) signal, desto högre hastighet ger algoritmen. Faktum är att om signalen är gles nog kan algoritmen helt enkelt sampla den slumpmässigt istället för att läsa den i sin helhet.

– I naturen är de flesta normala signaler glesa. Tänk till exempel på en inspelning av ett stycke kammarmusik: Den sammansatta signalen består endast av ett fåtal instrument som var och ett bara spela en ton i taget. En inspelning, å andra sidan, av alla möjliga instrument som var och spelar alla möjliga toner samtidigt skulle inte vara gles – men inte heller skulle det vara en signal som någon skulle bry sig om, säger Dina Katabi, en av den nya algoritmens utvecklare.

Den nya algoritmen, som Katabi och Piotr Indyk, båda professorer vid MIT:s Computer Science and Artificial Intelligence Laboratory (CSAIL), utvecklat tillsammans med sina elever Eric Pris och Haitham Hassanieh, bygger på två grundläggande idéer. Den första är att dela upp en signal i smalare ”skivor” (slices) bandbredd, med storlek så att en skiva i allmänhet kommer att innehålla endast en frekvens med tung vikt.

I signalbehandling är det grundläggande verktyget för att isolera vissa frekvenser ett filter. Men filter tenderar att ha suddiga gränser: Ett spektrum av frekvenser kommer att passera genom filtret mer eller mindre intakta; frekvenser strax utanför detta intervall kommer att vara något dämpade o frekvenser utanför intervallet kommer att dämpas ännu mer, och så vidare, tills du når frekvenser som filtreras bort nästan helt och hållet.

Om det så skulle hända att en frekvens med en tung vikt ligger vid kanten av filtret kan den bli så försvagad att det inte kan identifieras. Så forskarnas första insats var att hitta ett beräkningsmässigt effektivt sätt att kombinera filter så att de överlappar varandra och se till att inga frekvenser inom målområdet kommer att vara onödigt dämpade, men att gränserna mellan ”skivorna” av spektrum fortfarande är ganska skarpa.

När väl en ”skiva” av spektrumet har isolerats måste dock forskarna fortfarande kunna identifiera de mest viktade frekvenserna inom den ”skivan”. Enligt SODA-artikeln gör de detta genom att upprepade gånger skära spektrumskivan i mindre bitar och bara behålla dem där mest signaleffekt är koncentrerad. Men i en ännu så länge opublicerad artikel, beskriver de en mycket mer effektiv teknik, som lånar en signalbehandlingsstrategi från 4G-mobilnät. Frekvenserna är generellt representerade som”up-and-down squiggles” (slumpmässigt böljande linjer), men de kan också betraktas som oscillationer. Genom att sampla samma ”skiva” bandbredd vid olika tidpunkter, kan forskarna bestämma var den dominerande frekvensen finns inom den oscillerande cykeln, enligt ett pressmeddelande.

Mer information kan hämtas via den här länken .

Filed under: Utländsk Teknik