Med lämplig kodning och modulation kan man maximera antalet  överförda bitar över en fiber.  Men det gäller att göra avvägningar för att inte få intersymbolinterferens.

I jakten på att utnyttja befintlig, begränsad bandbredd på effektivast möjliga vis måste vi vara medvetna om att den komplexa modulerade signalen kan bli spridd i tid och att på varandra följande symboler kan överlappa varandra. Det kallas för intersymbolinterferens (ISI) . ISI inducerar fel i tolkningen av signalen på mottagarsidan. I frekvensdomänen måste vi också vara noga med att undvika störningar mellan angränsande kanaler. För minst 400 Gbit/s och 1 Tbit/s data kommer det att bli en fråga av avgörande betydelse.
Den här artikeln beskrivs de villkor som behövs för att förebygga dessa effekter och på användningen av olika filtreringsmetoder för att bandbredd och signalinneslutning.

Nyquistkriteriet
Den svenska ingenjören Harry Nyquist förklarade på 1920-talet att impulssvaret h (t) måste uppfylla följande krav i tidsplanet för att eliminera ISI: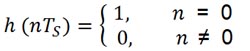

för alla heltal n. T_S är ett pulsavstånd av intilliggande pulser.
Fig 1, där en signal uppfyller detta villkor – sinc (t) pulser, illustrerar effekten av kriteriet: Pulserna överlappar varandra, men bara den samplade symbol bidrar till svaret vid samplingsögonblick t_k. De andra symbolerna är noll vid denna tidpunkt. På så sätt har vi undvikit de signalförsämringen och fel på grund av ISI.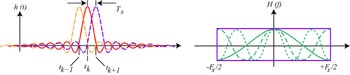

Fig 1. Ortogonala pulser av typen sinc (t) =sin(t)/t uppfyller Nyquist ISI-kriterium. [2]

Den högra sidan av fig 1 visar Fourier-transformen (FT) av impulssvaret. Det syns att det frekvensomfång som passar in i ett rektangulärt frekvensfönster uppfyller Nyquist ISI-kriteriet: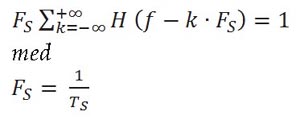

Det innebär att övertonerna, dvs frekvenskomponenterna som är en heltalsmultipel av den så kallade Nyquist frekvensen F_S,   måste läggas till ett konstant värde för att passa in i ett frekvensband utan ISI. Nyquistfrekvensen FS är den minsta bandbredd som krävs för att koda en signal utan att information går förlorad.

Nyquist-pulsformning med FIR- filter
En sinc-signal kan vara perfekt för att förhindra ISI som beskrivits ovan, men det är inte praktiskt eftersom den förlängs i oändlig tid. Därför behöver vi trunkera den i tidsdomänen, vilket i praktiken utförs genom att använda ett filter med finit impulssvar. Ett sådant FIR-filter, av ordning R, svarar på R + 1 samplingar för att sedan återgå till noll. Bara de senaste samplingspunkterna, x[n-1],tas hänsyn till vid faltningen av filterutgångens y [n], så att filtrering kan utföras i realtid.
Den tidsdiskreta FIR filter output y [n] i beroende av den ingående x [n] är beskriven av: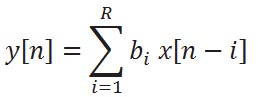

där bi är filterkoefficienterna.
För att undvika vikning (aliasing), måste det pulsformande FIR-filtret översamplas med minst en faktor q = 2. Med andra ord måste det finnas minst två samplingspunker inom T_S, så att pulsformen kan rekonstrueras på mottagarsidan utan att förluster av högre frekvenskomponenter.
Fig 2 visar filtersvaren för en sinc-puls som är filtrerade vid olika filtertal R, alltid översamplade med en faktor q = 2. Effektspektrum är ett resultat av  faltningens rektangulära spektrum av sinc-pulsen med det rektangulära fönstrets sinc-formade spektrum.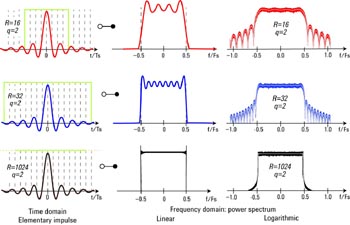

Fig 2. FIR-filter med olika tal R används för att korta av sinc-signaler. Här ser vi vågformen i tidsdomän samt vågformerna i effektspektrum efter Fast Fourier-transformation, i linjär respektive logaritmisk skala [2]

På första raden, med en filterordningen 16, sträcker sig signalen 8 T_S. Ur FFT framgår förvrängningar som orsakas av den begränsade tiden. Det mesta av effekten ligger inom Nyquist-bandet (-0,5 F_S till 0,5 F_S), men en del ligger utanför bandet.
Effektspektrumet visar ett spektrum av övertoner.
Om vi ​​fördubblar längden på filtret (R = 32) ryms signalen bättre inom bandbredden, men vi ser fortfarande en del ringningar.
Vid R = 1024 ser spektrum nästan ideal ut: Ringningen är endast synligt på de branta flankerna och effektspektrumet visar också mindre bidrag utanför frekvensbandet.
Olyckligtvis leder högre ordningens R hos filtret till filterkonstruktioner med högre komplexitet. Därför bör man nöja sig med det lägsta R som motsvarar kraven.

"Raised cosine"-filter
För ännu bättre utombandsdämpning och ett spektrum utan ringningar är "raised cosine"-filter ett tänkbart alternativ. Här är pulssvaret beroende av den så kallade ”roll-off”-faktorn α som kan ha vilket som helst värde från 0 till 1: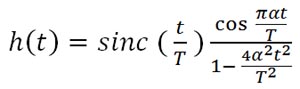

"Raised-cosine"-filter uppfyller även Nyquist ISI-kriteriet i det att att endast den samplade symbolen bidrar till signalen. Alla andra symboler är noll vid samplingspunkterna. I jämförelse med sinc-formade pulser kräver raised-cosine-signaler mer bandbredd.
Fig 3 visar filtersvaret för fyra olika roll-off faktorer: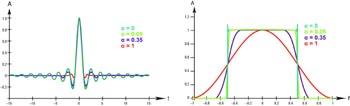
                
Fig 3. Raised-cosine-filter med olika roll-off faktorer, här visade i  normaliserad tids- respektive frekvensdomän [2].

I frekvenssvaret  framgår att för varje värde av α kommer kurvorna att passera samma punkt, ±T_s/2, dvs halva pulshastigheten. Såsom nämnts tidigare är detta Nyquist-frekvensen, den minsta bandbredd som krävs för en dataöverföring utan förlust av information.
Bortsett från detta kan du se att för α= 1 har vi knappast någon ringning men frekvensspektrat passar inte in i bandbredden.
För α = 0, är ​​det tvärtom: svarsfrekvensen är rektangulär inom bandbredden (döverslängarna i kanterna är snarast en matematisk effekt, även känd som Gibbs fenomen, och inte har någon praktisk betydelse). Trots det visar tidsdomänsignalen ännu större ringning.
Varför ska vi bry oss om ringningen när vi först slog fast att bara den samplade symbolen bidrar till signalen vid samplingspunkten?
I praktiken är det ett problem eftersom de andra symbolerna ger ett nollbidrag enbart om samplingen utförs under denna ideala ögonblick. Under verkliga förhållanden är det nästan omöjligt att få mottagaren att sampla  vid denna tidpunkt. Därför kommer vi alltid att ha några ISI som inducerar fel vid tolkningen av signalen.
Så, vi har uppenbarligen en kompromiss mellan bandbredd inneslutning och undertryckande av ringningar i tidsdomänen.
Vi måste därför finna en  kompromiss i valet av ett lämpligt värde av a på individuell basis för varje fiberoptisk applikation.

Raised-cosine-filter i praktiken
Vi kommer att ta en närmare titt på påverkan av olika roll-off faktorer på exemplet med det mest lovande moduleringsschemat för 400 Gbit/s och högre datahastighet: 16 QAM. Vi mätte inte bara frekvensdomänsvar utan granskade även ögondiagram och påverkan på övergångarna mellan konstellationspunkter och konstellationspekarna  själva (se Figur 4).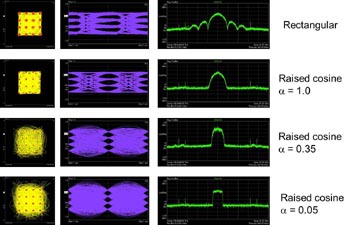

Fig 4. Raised-cosine-filter på en 16 QAM-signal påverkas av roll-off-faktorn a: Konstellationsdiagram, ögondiagram och frekvensspektrum visar signaler som skapats med en Agilent M8190A vågformsgenerator för generella (arbitrary) vågformer.

Den översta exempel visar fallet med icke-formade rektangulära pulser. Som vi vet har en signal som bara upptar ett fast tidsintervall ett oändligt utsträckt frekvensspektrum. Och, faktiskt, kan vi se det i frekvensgången för de stora sidoflankerna. Ögondiagrammets öppna ögon visar det typiska beteendet hos en bredbandig signal. Mellan konstellationspunkterna, har vi raka övergångar.
Med hjälp av ett raised-cosinusfilter med en roll-off faktor α= 1 blir frekvensspektrum smalare. Flankernas lutningar syns inte längre. Ögondiagrammet visar vidöppna ögon. Konstellationspunkterna är mindre. Detta är typiskt för ett system med reducerad bandbredd. Detekterings bandbredden på mottagarsidan är underförstått också minskad vilket sänker bruset.
Vid en roll-off faktor α= 0,35, har frekvensbredden ytterligare minskat, och därmed storleken av konstellationspunkterna.
Övergångarna mellan konstellationspunkterna börjar visa stora överslängar. Det beror på att tiden förlängs då man minskar bandbredden hos övergångarna mellan symbolerna. Detta återspeglas i konstellationsdiagrammet av långa böjda övergångar mellan punkterna. Ögonen stänger och därmed blir samplings-timingen mer kritisk.
Ett nästan perfekt rektangulärt spektrum nås vid α= 0,05. Övergångarna mellan de små konstellationspunkterna visar stor översvängning. Den helt slutna ögon tyder på att för att undvika fel, har provtagningspunkt justeras exakt.

Hur mycket spektral effektivitet vinner vi?
För att få en uppfattning om den kvantitativa vinsten i spektral effektivitet genom pulsformningsfilter jämför vi med den effekt som nås genom att tillämpa Orthogonal Frequency Division Multiplexing (OFDM).
Fig 5 ger en kort resumé av OFDM-principer, som liknar den Nyquist-format.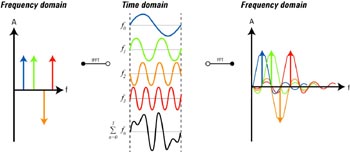

Fig 5. OFDM i frekvens- och i tidsdomänen [2]

I OFDM är subfrekvensspektrum sinc-format. För ökad spektrumeffektivitet finns det överlappning men på grund av deras ortogonalitet,  vilket innebär att de förskjuts av multipler av π/2, att de inte stör varandra. I tidsdomänen är en symbol en summa av sinuskurvor med ekvidistanta bärvågsfrekvenser F_n i ett bestämt tidsfönster. I det här exemplet har vi i en kanal 4 underbärvågor vid 4 frekvenser. Den orangefärgade kurvan är fasförskjuten, som kan ses efter invers snabb Fourier-transformation (IFFT).
Fig 6 visar nu spektralanalys på en uppmätt 16-QAM-modulerad OFDM-signalen.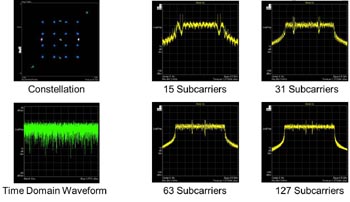

Fig 6. Effekter av OFDM på en 16-QAM-signalspektrum i beroende av antalet underbärvågor; signaler som skapats med en Agilent M8190A godtycklig Vågformsgenerator.

Längst upp till vänster kan du se konstellationsdiagrammet och därunder vågformen i tidsdomänen.
Med 15 underbärvågor och två pilotsignaler får vi ett ganska platt frekvensspektrum och en brant roll-off.
Genom att öka antalet underbärvågor, plattas spektrum till och de två pilotsignalerna är på väg mot mitten. På den nedersta raden ser vi att spektrum närmar sig rektangulär format, med det växande antalet underbärvågor.

Hur stor blev vinsten?
Hur kan man nu översätta detta i en vinst i spektral effektivitet i jämförelse med det som uppnås med pulsformning enligt Nyquist?
För jämförbarhetens skull visar figur 7 hur  den normaliserade spektrumeffektiviteten SE ritas över Nyquist filterlängden R (översamplingsfaktorn q väljs åter till 2) kontra antalet OFDM-underbärvågor N.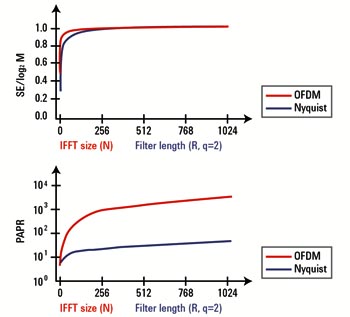

Fig 7. Effekten av pulsformning enligt Nyquist kontra OFDM i fråga om spektrumeffektivitet och förhållande topp-till-medeleffekt (PAPR) [2]

Figuren visar att båda teknikerna ger nästan samma resultat avseende spektrumeffektivitet.
Jämförelsen av de också normaliserade förhållandet topp-tillmedeleffekt  (PAPR) visar liknande beteende på olika nivåer. PAPR av OFDM-tidsdomänens vågformer är mycket större. Ett faktum är att OFDM-signalen uppvisar vissa toppvärden, högt över den genomsnittliga effektnivån.
Följaktligen behöver testinstrument för OFDM-kretsar ett stort dynamiskt omfång för att undvika distorsion som förs in genom att de högre nivåerna klipps.
För att utnyttja spektrum optimalt kan pulsformning tillämpas i kombination med OFDM.
Stephanie Michel

Artikelförfattaren är teknisk marknadsföringsingenjör inom Digital Photonic Test Division of the Electronic Measurements Group hos Agilent Technologies.

Referenser:
[1] H. Nyquist: Vissa ämnen i Telegraph Transmission Theory, Trans. AIEE, vol. 47, pp 617-644, april 1928
[2] R. Schmogrow M. Winter, M. Meyer, D. Hillerkuss, S. Wolf, B. Baeuerle, A. Ludwig, B. Nebendahl S. Ben-Ezra, J. Meyer, M. Dreschmann, M. Huebner, J . Becker, C. Koos, W. Freude, och J. Leuthold,: Real-Time Nyquist Pulse Generation Beyond 100 Gbit / s and it´s relation to OFDM, Optics Express, Vol. 20 (1), pp 317-337, januari 2012

Filed under: Opto