Provningsteamet hos halvledartilvlerkaren ams har utvecklat en standardprovningsrutin för både karakterisering och produktion av IC. Metoden är att använda en chirp-signal för att frekvenssvepa ett filter och detta görs i en engångsmätning. Den beskrivs här av Peter Sarson, provnings- och utvecklingschef samt Andreas Wild, marknadschef, affärsenheten för halvledartillverkning (Full Service Foundry) inom ams AG.

Personer som arbetar med utveckling av IC-kretsar (integrerade kretsar) har inte större möjligheter att förutse framtiden än någon annan. I teorin kan en ny IC-krets tas i produktion med fullständiga specifikationer och väl definierade egenskaper, men i praktiken är det vanligt att ytterligare krav eller specifikationer tillkommer efter att produktionsprocessen har startat.
IC-produktionsteamen kan oftast hitta sätt att införliva senkomna önskemål från utvecklarna. Ett vanligt och problematiskt exempel är det vanliga önskemålet att ändra den karakterisering som RF-filtren har tilldelats av produktionsprovningsenheten. Ändringen innebär omfattande ändringar av den programkod som används vid provningen. Provningsprocessen försenas och dessutom fördröjs utvecklingen av chip-set så att tape-out-steget (sista steget i konstruktionen före produktion) försenas, samtidigt som det finns risk att tillföra nya fel i provningens programkod. Det är vanligt att hela produktionsteamet befinner sig under press på att snabba upp tillverkningsprocessen, och det finns inte alltid tillräcklig tid för omfattande avbuggning av provningskoden.

Ny metod för provning
Provningsteamet hos ams försökte därför ta reda på om ett nytt tillvägagångssätt vid karakterisering av RF-filter skulle kunna eliminera det här problemet. Teamets strategi var att utveckla en standardprovningsrutin som samtidigt skulle kunna användas för både karakterisering och produktion. Det var även nödvändigt att kunna utföra vissa enkla modifieringar av rutinen, för att anpassa den till en mängd olika IC-kretsar. Den nya rutinen skulle lagras i ett bibliotek för provningskoder, något som skulle underlätta upprepad återanvändning av en grunduppsättning provnings-IP.
Metoden som undersöktes var en chirpmetod som innefattade ett svep av filtrets frekvensintervall och utförde karakterisering i en engångsmätning.

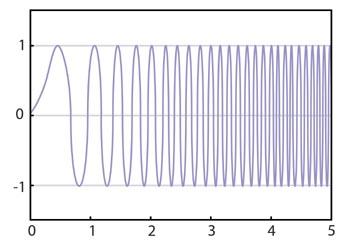
Fig 1. En chirp-signal innebär ett frekvenssvep.

Teamet tittade på möjligheter att använda en multitonsignal för att karakterisera filtren. Den lösningen är dock olämplig för enheter med låg ineffektkänslighet. För att använda multiton måste varje frekvenskomponent divideras med det totala antalet frekvenser, så att det totala förhållandet mellan toppvärde och effektivvärde (crest-faktorn) är lägre än den maximala ineffekten. Om detta inte görs påverkar de individuella frekvenserna varandra och orsakar intermodulation och distorsion som kan förvränga resultaten vid frekvenssvepet.

Så här byggs en chirpsignal
Vid en chirp-signal (signalöverföring med hörbara ljud) ökar signalens momentana frekvens linjärt utan några frekvenshopp (se fig 1). Om en provningstekniker vill implementera en chirp-signal i praktiken måste hänsyn tas till det begränsade minnet hos en AWG-generator (Arbitrary Waveform Generator, dvs en generator för godtycklig vågform) – det blir alltså nödvändigt att skapa en chirp-enhet i diskret form.
Formeln för linjär chirp definieras av ekvationen f_(t) = f₀ + kt, där f₀ är startfrekvensen (vid tidpunkten t = 0), och k är frekvensökningens hastighet, eller chirp-hastigheten.
Efter chirp-svep och inläsning av resultaten krävde den nya metoden också ett sätt att extrahera den viktigaste parametern som IC-konstruktörerna vill karakterisera: magnitudrespons, dvs 3 dB-punkten, 10 dB-punkten samt filtrets bandbredd. Andra parametrar som ibland också begärs är fasrespons och gruppfördröjning.

Bygg en chip-vågform
När en chir-psignal ska byggas in i DSP är det viktigt att förstå flera parametrar:
* Vilken noggrannhet krävs vid mätningen av bandpassfiltrets brytfrekvenser?
* Vilka funktioner i provningsinstrumentet stöder mätningen – minnesdjup, maximal samplingsfrekvens, fusionering av vågformer?
* Vilka är filtrets brytfrekvenser och vilken bandbredd har filtret?
Med den syntax som finns tillgänglig i de senaste verktygen för utveckling av provningskod är det ganska smidigt att bygga en chirp-vågform i DSP. Syntaxen ger i regel möjlighet att bygga en sinusvågform med hjälp av inbyggda funktioner (BIF – Built-In-Functions) som bygger på antal samplingar, samplingsfrekvens, matrisens dimension, fasfördröjning och Sinx/x-korrigering.
När den här koden läggs in i en loop och bin-numret ökas linjärt, genereras en uppsättning vågformer med en linjär ökning av tonfrekvensen (Ft). Så länge som koherensen garanteras, genom garanti att samplingsteoremet uppfylls, kan dessa vågformer fusioneras tillsammans och skapa en diskret chirpsignal.

IFFT
Om det inte finns några inbyggda funktioner (BIF) för generering av de individuella vågdelarna kan dessa skapas enkelt genom användning av samplingsteoremet. Detta kräver en matris där M ökas linjärt och en inverterad Fast Fourier-transform (FFT) utförs, på följande sätt:
Ekvation för samplingsteorem: F_s/F_t = N/M
Ekvation för beräkning av Fourier-frekvens: F_f = F_s/N
När den inverterade Fast Fourier-transformen har skapats måste tidsdomändata för varje segment fusioneras med de övriga data för att ta fram en enda array med en storlek som motsvarar antalet toner multiplicerat med antalet samplingar. Här är det viktigt att se till att matrisen inte är större än AWG-enhetens minne.
I den chirp-provning som togs fram för de kunder som beställer halvledarsystem från ams mättes sämsta tänkbara fall. Detta fall avsåg ett filter med smalast tänkbara bandbredd, vid en centrumfrekvens på 40 kHz och en bandbredd på cirka 80 kHz. De låga respektiva höga 3 dB-punkterna måste mätas med en noggrannhet som är bättre än 5 kHz.
Med detta sämsta tänkbara fall som underlag byggdes en chirpenhet som hade 100 diskreta frekvenser med en frekvensupplösning på 1 kHz. Chirp-signalen startade vid en frekvens på 1 kHz och avslutades vid 100 kHz. Se fig 2.

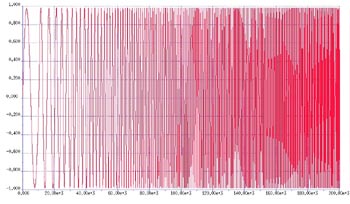
_{Fig 2. Normaliserad chirpsignal.}

En studie av beteendet hos den här signalen i den frekvensdomän som visas, oberoende av om frekvensresponsen stämde överens med förväntning på ett plant spektrum från 1 kHz till 100 kHz, eftersom signalens magnitud är oförändrad under svepet. När en Fast Fourier-transform (FFT) utförs på en genererad chirpsignal visas frekvenssvaret (se fig 3) – ett plant svar ger en frekvensdomän som stöder inläsningen av exakta relativa mätningar, t ex 3 dB-punkter.

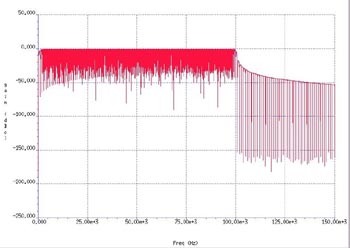
Fig 3. FFT för chirpsignalen.

När signalen har genererats är nästa steg att mäta den. För att jämförelsen ska bli lättöverskådlig är det lämpligt att läsa in samma antal punkter, och använda samma samplingsfrekvens, dels vid mätsteget och även vid det steg då signalen skapas. Fig 4 visar en momentanvärde för karakteristikkurvan hos ett bandpassfilter. Med utgångspunkt i DSP-analysen från det här resultatet kan 3 dB-punkterna beräknas.

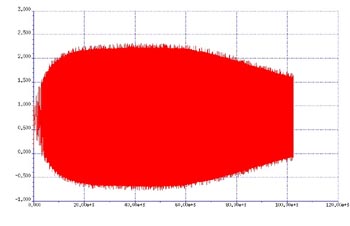
Fig 4. Momentant tidsdomänvärde.

Efter att en Fast Fourier-transform (FFT) har utförts på den inlästa matrisen (se fig 5) kan filtrets exakta 3 dB-punkt beräknas med hjälp av DSP och följande sekvens:
1) Utför en viss genomsnittsberäkning för att jämna ut matrisen. Detta ser till att det inte uppstår några kraftiga förändringar i matrisen.
2) Konvertera den inlästa matrisen från volt till dBc.
3) Lägg till 3 dB till hela matrisen. -3 dB-punkten är nu vid 0 dB.
4) Exekvera en klipp-array runt ± ett mycket litet värde.
5) Utför xtrm-analys på den klippta matrisen. Detta lokaliserar matrisen för lågpassfiltrets 3 dB-punkter.
6) Reverserad matris: detta sätter filtrets högpassdel i början av matrisen.
7) Utför xtrm-analys på den reverserade klippta matrisen. Detta lokaliserar matrisen för högpassfiltrets 3 dB-punkt. Det är viktigt att komma ihåg att det här värdet ska subtraheras från det totala antalet punkter.
8) Multiplicera matrisernas värden med Fourier-frekvensen (Ff): resultaten är sedan ±3 dB-punkter uttryckta i Hz.
9) Subtrahera 3 dB-punkternas värden: det här resultatet ger filtrets bandbredd.

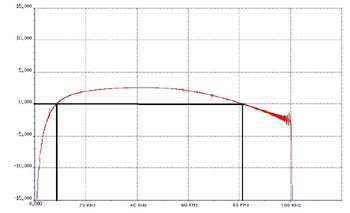
Fig 5. Frekvensdomänkarakteristik för matrisen i fig 4.

Om provningsprogrammet som beskrivs ovan är robust kommer det att finnas ett exakt samband mellan referensresultatet och resultaten från produktionsprovningen. I exemplet som visas här har mätningen av den övre gränsfrekvensen ett mycket stabilt resultat på 84,3 kHz med en standardavvikelse på 36 Hz (se fig 6).

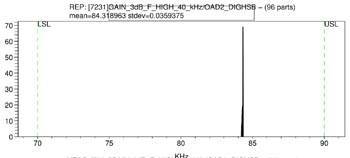
Fig 6. Repeterbarhet för 40 kHz-bandpassfiltrets övre gränsfrekvens.

Fig 7 visar att det finns en nära koppling mellan resultaten från referensprovningarna och produktionsprovningarna. Kombinerat med stabilitetsdata visar detta att provningsprogrammet som beskrivs ovan ger ett idealiskt strategi för produktionsprovning av RF-IC-kretsar.

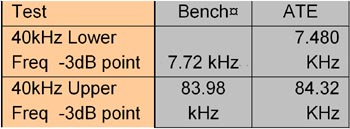
Fig 7. 40 kHz filterkorrelation.

Återanvänd IP
Den här artikeln började med att beskriva ams-programmets mål. Syftet var att generera ett provningsprogram vars IP kan återanvändas över flera projekt. Strategin för återanvändningen var att basera programmet på en normaliserad vågform som gick från 1 kHz till 100 kHz i steg om 1 kHz. Eftersom vågformen är normaliserad till 1 kHz kan upplösningen enkelt skalas upp genom en uppsampling av vågformen – dvs genom ökning av AWG-enhetens samplingsfrekvens.
Fourierfrekvensen på 1 kHz användes för ett 40 kHz-filter där 3 dB-punktens karakterisering behövde hålla en rimlig noggrannhet. Samma vågform, som redan har lästs in i AWG-enhetens minne, kan användas för andra filter genom ökning av Fs, vilket sparar AWG-minne. Filtret med det högsta frekvensintervallet i den här tillämpningen hade en centrumfrekvens på 550 kHz och en 3 dB-punkt på cirka 800 kHz. Om Fs multipliceras med 10 produceras en vågform med en Fourier-frekvens på 10 kHz i stället för 1 kHz. Chirp startar nu vid 10 kHz och slutar vid 1 MHz. Fig 8 visar hur den här metodiken ger ett acceptabelt samband.

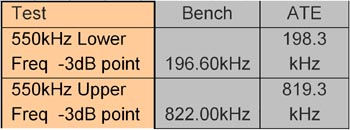
Fig 8. 550 kHz filterkorrelation.

En jämförelse av mätresultatet med källvågformen visar att felet är mindre än källvågformens upplösning (upplösning = 10 kHz, fel = 3 kHz). Detta beror på att klippfunktionen används, och dess beteende liknar en interpolering.
Om en chirpsignal med en god Fourier-frekvensupplösning används kan en god korrelation uppnås i karakteriseringssyfte. Om signalen utformas på ett sätt där den kan normaliseras kan samma vågform också användas för högre frekvenser med lägre upplösning baserat på manipulering av AWG-enhetens samplingsfrekvens, vilket gör detta tillvägagångssätt extremt flexibelt och lämpligt för många olika enheter.

Författarna
Peter Sarson är provnings- och utvecklingschef på avdelningen Full Service Foundry inom ams AG. Han tog kandidatexamen i teknologi med högsta betyg på universitetet i Sheffield i Storbritannien år 1998. Han har arbetat inom automatiserad provningsteknik under 13 år.
Andreas Wild är marknadschef inom halvledartjänster och halvledarteknik på avdelningen Full Service Foundry inom ams AG.
Andreas arbetade först på ams avdelning för konstruktionssupport i åtta år och sedan nio år tillbaka arbetar han med marknadsföring av halvledarsystem.
Författarna kan kontaktas på e-postadressen foundry@ams.com.

Filed under: Mikrovag