I det här exemplet diskuteras kortfattat hur övergången mellan en koaxialkontakt och en mikrostripp kan optimeras med hjälp av AWRs EM-simulator Analyst som arbetar med finita element (FEM) i tre dimensioner.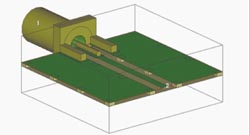

När man jämför mätresultat med simulerade resultat betraktas övergången (fig 1) från mäthårdvarans koaxialkabel till testobjektets signalväg vanligen som ideal. Men i verkligheten ger idealiseringen avvikelser mellan simuleringsdata och uppmätta data vid högre frekvenser.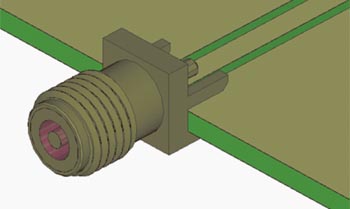

Fig 1. Via en SMA-kontakt ansluts mäthårdvarans koaxialkabel till kretskortet, och koaxialkabelns signal övergår till en signal i mikrostrippen som går till testobjektet.

Antagandet om ideala förhållanden görs implicit så snart som simuleringens in-/utportar finns i signalvägen, t ex på mikrostrippen eller koplanarvågledaren (fig 2). Även om det finns ett flertal metoder som kan användas för att säkerställa att övergången får så låg reflexion som möjligt, belyser det här speciella exemplet hur man kan använda en fullständig tredimensionell elektromagnetisk FEM-modell av kontakten. Då kan man hantera övergångens parasiter analytiskt, slippa idealisera och komma närmare verkligheten.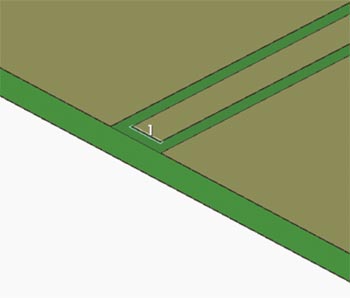

Fig 2. Typiskt sitter simuleringsporten direkt på mikrostrippen. Om man simulerar utan att ta hänsyn till diskontinuiteten som representeras av kontakten i fig 1, får man systematiskt annat resultat vid simulering än vid mätning.

Konstruktionen
I schemat (det överordnade dokumentet) har vi ritat ett kretskort med en signalväg. Den tredimensionella kontakten som är konstruerad för 20 mil-substrat är tekniskt uttryckt en submodell underordnad det överordnade dokumentet, d v s konstruktionen är hierarkisk. Kontaktmodellen gör att man kan placera en port i koaxialkontaktens koaxialkabelände (inporten) och definiera den andra porten som en vågport i änden av mikrostrippen (utporten). Utportens referensplan flyttas till direkt efter kontakten.

Övergångens kvalitet utan optimering
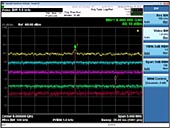
Övergångens S11-parameter (fig 3) visar att anpassningen är bra bara upp till ca 2 GHz. Vid konstruktionsfrekvensen 10 GHz är reflexionen så hög som -10 dB. Tydligen skulle konstruktionen gynnas av en optimerad övergång – inte bara på grund av energiförluster utan även på grund av att missanpassningen ger en avsevärd skillnad mellan uppmätta och simulerade värden.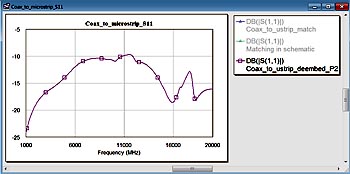

Fig 3. Övergångens reflexionskoefficient vid koaxporten före optimering.

Optimeringsstrategi
Modellen av övergången kan optimeras i schemaform med hjälp av EM-dokumentet som en vanlig submodell. Det är enkelt att se att optimeringen vid 10 GHz kan göras med anpassningskrets med serieinduktans och parallellkapacitans. I mikrostrippen kan en serieinduktans realiseras med ett smalt ledarsegment, och en parallellkapacitans kan realiseras med ett brett ledarsegment. Se fig 4. Det är enkelt att optimera ledarens dimensioner.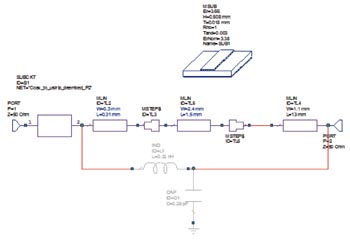

Fig 4. Ansats till anpassningskrets för optimering av övergången från koax till mikrostripp.

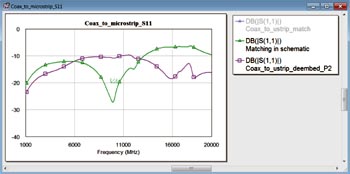
Fig 5. Reflexionskoefficienten för övergången vid koaxporten vid användning av sluten-form-modellerna av anpassningskretsen (grön kurva).

Det sista steget är att lägga in anpassningskretsens dimensioner i 3D-modellen och köra en verifieringssimulering enligt fig 6.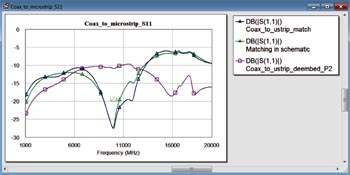

Fig 6. Reflexionskoefficienten för övergången vid koaxporten inklusive en fullständig tredimensionell modell av anpassningskretsens geometri (blå kurva).

Det framgår att det första anpassningsförsöket är utmärkt.

Det är instruktivt att betrakta en bild av ytströmmarna vid 10 GHz. Se fig 7.

Fig 7. Ytströmmen i den optimerade övergången vid 10 GHz.

Sammanfattningsvis får man med en enkel anpassningskrets en signalövergång från koaxialkabel till mikrostripp med mindre än -20 dB reflexion vid konstruktionsfrekvensen 10 GHz. Den användbara bandbredden är ca 2 GHz, och det är enkelt och tillförlitligt optimerat med konventionella kretsmodeller och EM-modellen av kontakten. En fullständig tredimensionell EM-lösning är lätt att få fram med den optimerade geometrin.
Modeller av övergångar från olika kontakter till olika kortsubstrat kan lagras i form av ett bibliotek och enkelt användas i det fortsatta kretskonstruktionsarbetet. Det integrerade tredimensionella EM-verktyget gör att man kan ha alla konstruktionsdata i samma fil i konstruktionsmiljön AWR Design Environment (AWRDE), inklusive kontakter, kapslade moduler, höljen eller andra godtyckliga tredimensionella föremål. Det eliminerar risken för felaktig användning, t ex i fall där en vågrät kontakt byts ut mot en lodrätt.
Den grafiska vyn av konstruktionen visar omedelbart vilken 3D-modell som används, detta till skillnad från fallet där kontaktens S-parametrar beräknas utanför programmet och importeras som en ren datafil till AWRDE. Med alla data i samma projektfil får man också enklare dokumentering, överföring, lagring och återanvändning av konstruktionen.

Filed under: Utländsk Teknik